TRIANGLE/POINT

To test if a point is inside a triangle, we compare the area of the original triangle with the sum of the area of three triangles made between the point and the corners of the triangle.

Here's a diagram demonstrating the triangles created for a point outside and inside the triangle:

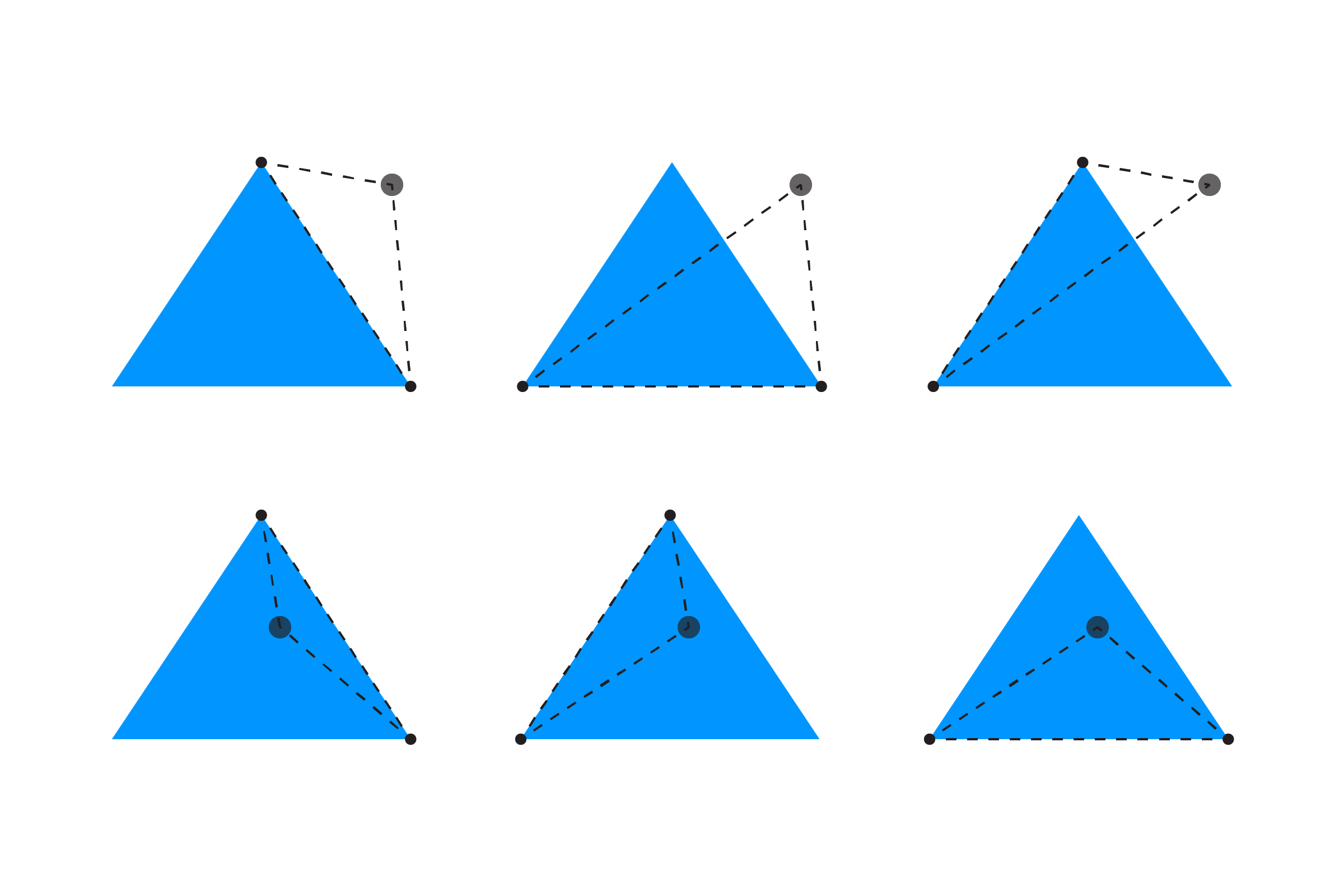
Points outside and inside a triangle, forming three smaller triangles

To get the area, we use Heron's Forumula:

var areaOrig = abs( (x2-x1)*(y3-y1) - (x3-x1)*(y2-y1) );

We need to calculate the area of the three triangles made from the point as well:

var area1 = abs( (x1-px)*(y2-py) - (x2-px)*(y1-py) );
var area2 = abs( (x2-px)*(y3-py) - (x3-px)*(y2-py) );
var area3 = abs( (x3-px)*(y1-py) - (x1-px)*(y3-py) );

If we add the three areas together and they equal the original, we know we're inside the triangle! Using this, we can test for collision:

if (area1 + area2 + area3 == areaOrig) {
    return true;
}
return false;

Here's a full example:

var px = 0; // point (set by mouse)
var py = 0;
 
var x1 = 300; // three points of the triangle
var y1 = 100;
var x2 = 450;
var y2 = 300;
var x3 = 150;
var y3 = 300;
 
function setup() {
    var canvas = createCanvas(600, 400);
    canvas.parent("sketch");
 
    noCursor();
 
    strokeWeight(5); // make point easier to see
}
 
function draw() {
    background(255);
 
    // mouse point to mouse coordinates
    px = mouseX;
    py = mouseY;
 
    // check for collision
    // if hit, change fill color
    var hit = triPoint(x1, y1, x2, y2, x3, y3, px, py);
    if (hit) fill(255, 150, 0);
    else fill(0, 150, 255);
    noStroke();
    triangle(x1, y1, x2, y2, x3, y3);
 
    // draw the point
    stroke(0, 150);
    point(px, py);
}
 
// TRIANGLE/POINT
function triPoint(x1, y1, x2, y2, x3, y3, px, py) {
    // get the area of the triangle
    var areaOrig = abs((x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1));
 
    // get the area of 3 triangles made between the point
    // and the corners of the triangle
    var area1 = abs((x1 - px) * (y2 - py) - (x2 - px) * (y1 - py));
    var area2 = abs((x2 - px) * (y3 - py) - (x3 - px) * (y2 - py));
    var area3 = abs((x3 - px) * (y1 - py) - (x1 - px) * (y3 - py));
 
    // if the sum of the three areas equals the original,
    // we're inside the triangle!
    // (< 1 due to floating point issues in Javascript)
    if (Math.abs((area1 + area2 + area3) - areaOrig) < 1) {
        return true;
    }
    return false;
}

This example was built on a modified version of a post on YoYo Games. If you would like to read a lengthy discussion on the merits and problems with this method, and many other suggestions, see this thread on GameDev.net.