LINE/POINT

So far, our collisions have mostly been logic and a little bit of addition. Line collision is a little trickier, unless your high school geometry class is still fresh.

A line (see note) is defined by two sets of X/Y coordinates. We can find the length of the line using our old standby the Pythagorean Theorem, but since we'll need to use it three times in this example, let's cheat and use Processing's built-in dist() function:

var lineLen = dist(x1,y1, x2,y2);

We also need to figure out the distance between the point and the two ends of the line:

var d1 = dist(px,py, x1,y1);
var d2 = dist(px,py, x2,y2);

If d1+d2 is equal to the length of the line, then we're on the line! This doesn't make intuitive sense, but look at this diagram:

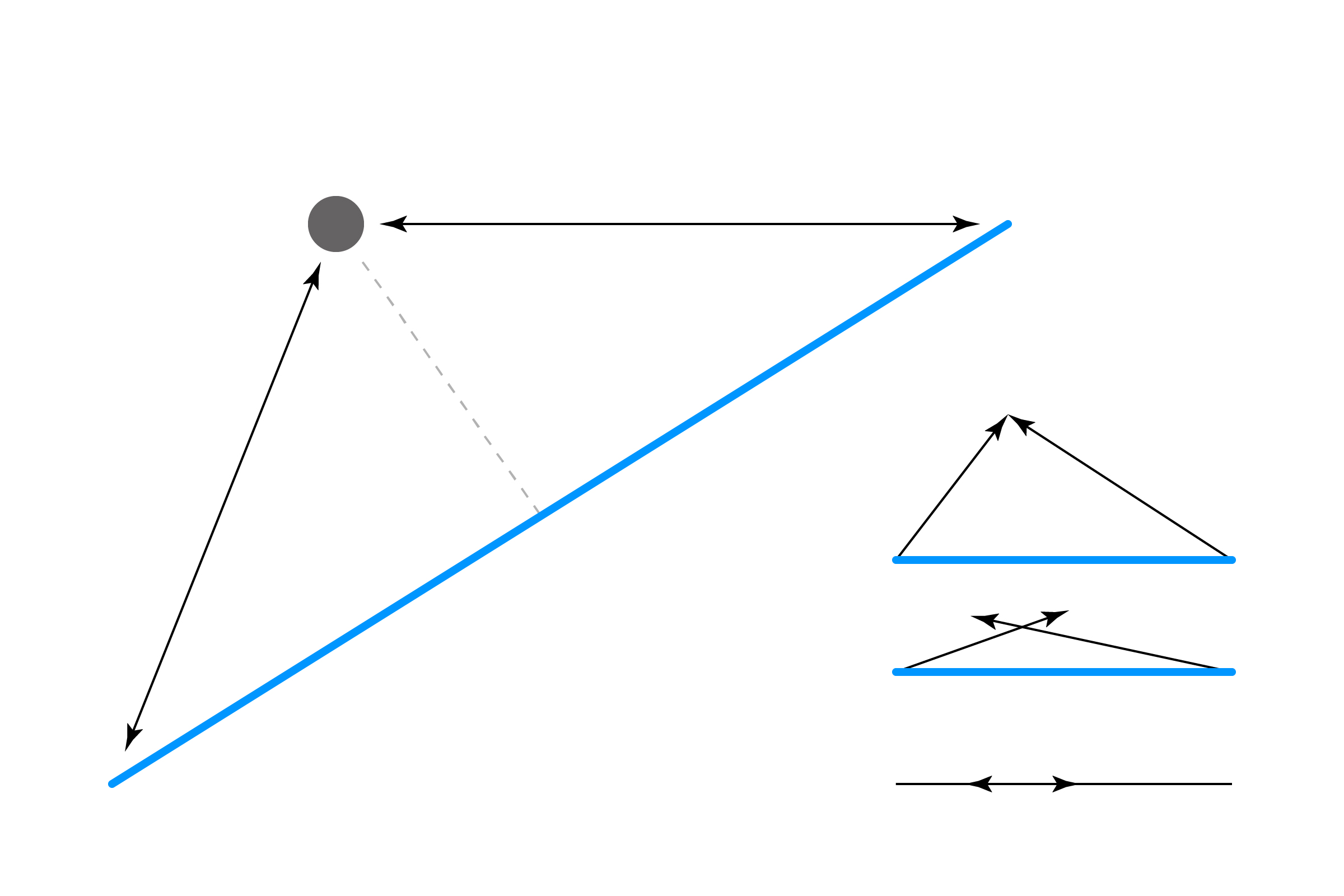
Forming triangles between a point and line

If we collapse the distances, they are longer than the line!

There's a bit of an issue here, though. Since floating-point numbers are so minutely accurate, the collision only occurs if the point is exactly on the line, which means we're not going to get a natural-feeling collision. This is very similar to our first example, Point/Point. To fix this, let's create a small buffer and check if d1+d2 is +/- that range.

var buffer = 0.1;   // higher # = less accurate collision

Try playing with this value until you get something that feels right. Using this buffer value, we'll check for a collision:

if (d1+d2 >= lineLen-buffer && d1+d2 <= lineLen+buffer) {
    return true;
}
return false;

Here's a full example, combining everything above:

var px = 0;     // point position (set by mouse)
var py = 0;
 
var x1 = 100;   // line defined by two points
var y1 = 300;
var x2 = 500;
var y2 = 100;
 
 
function setup() {
    var canvas = createCanvas(600,400);
    noCursor();
 
    strokeWeight(5);  // make things a little easier to see
}
 
 
function draw() {
    background(255);
 
    // set point to mouse coordinates
    px = mouseX;
    py = mouseY;
 
    // check for collision
    // if hit, change the color of the line
    var hit = linePoint(x1,y1, x2,y2, px,py);
    if (hit) stroke(255,150,0, 150);
    else stroke(0,150,255, 150);
    line(x1,y1, x2,y2);
 
    // draw the point
    stroke(0, 150);
    point(px,py);
}
 
 
// LINE/POINT
function linePoint(x1,y1, x2,y2, px,py) {
 
    // get distance from the point to the two ends of the line
    var d1 = dist(px,py, x1,y1);
    var d2 = dist(px,py, x2,y2);
 
    // get the length of the line
    var lineLen = dist(x1,y1, x2,y2);
 
    // since floats are so minutely accurate, add
    // a little buffer zone that will give collision
    var buffer = 0.1;    // higher # = less accurate
 
    // if the two distances are equal to the line's
    // length, the point is on the line!
    // note we use the buffer here to give a range,
    // rather than one #
    if (d1+d2 >= lineLen-buffer && d1+d2 <= lineLen+buffer) {
        return true;
    }
    return false;
}

* OK, technically this would be called a "line segment". But for the sake of simplicity, we'll be referring to these as the generic term "line". Haters to the left.

This algorithm is thanks to help from this answer by MrRoy on StackOverflow.